When two lines or rays come together they always create an angle, which’s an aspect, in geometry and various fields of science and engineering. We commonly use the term “angles” when discussing plane trigonometry, where straight lines intersect without any curves. This idea forms the basis of physical theories and practical uses. For instance angles like acute, obtuse and right angles each hold characteristics and meanings, in scenarios and constructions.
At the spot where the two straight lines meet, known as the vertex is where the angle originates. It exists without a boundary but extends from the vertex to where the two straight lines conclude or alter their form. Grasping this idea holds importance in fields such, as architecture, engineering and art since it influences how shapes and spaces are designed and understood.
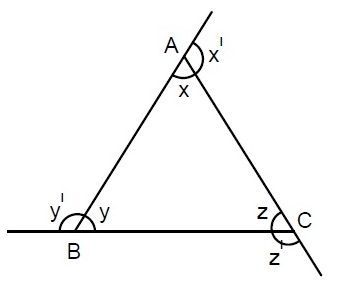
Angles are often compared in terms of their similarities or differences which can provide insights, into properties. This understanding is crucial for developing proofs and solving problems in physics and engineering. When two angles share a vertex and side they are referred to as angles. On the hand if they share a vertex but their sides extend in opposite directions they are known as opposite angles at the vertex. These opposite angles always have measures leading to two pairs of congruent angles. These angle relationships serve as the foundation, for theorems and principles.
This occurs because the angle may not exceed a rotation, which’s either 360° (degrees) 400 g (centesimal degrees) or 2π radians, at most. This idea of symmetry serves as a foundation for various principles in geometry and physics where rotational motions and symmetries are crucial. The angles that come together to form a revolution are known as supplementary while those that create a quarter turn are referred to complementary. Understanding these connections is essential, for solving trigonometric problems.
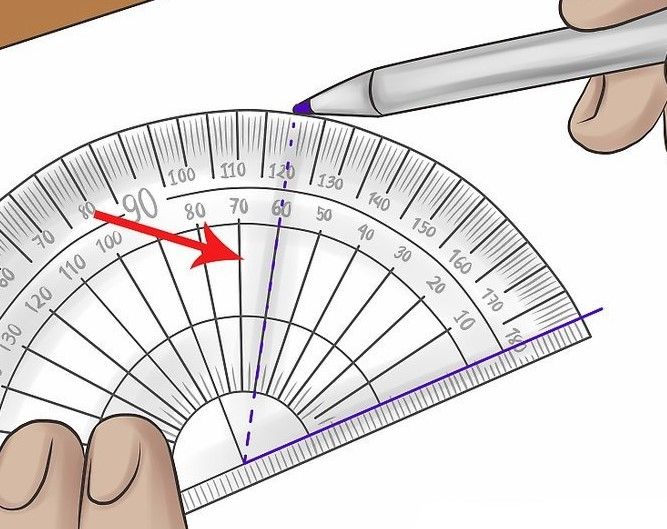
The concept of angle sizes forms the basis of trigonometry. Has always been vital, for practical mathematical uses; anything related to building and engineering projects relies on this kind of calculation. The ability to figure out and work with angles is crucial in designing and constructing buildings analyzing motion and in scientific and engineering fields. The primary tool for measuring an angles size is the protractor, which covers half of a rotation. Despite its simplicity the protractor plays a role, in teaching and applying angle measurement concepts.
The tool measures angles in degrees with a limit of 180°. This restriction reflects the circles division into two semicircles, a concept, in geometry. To use the protractor align its edge with one side of the angle. Read the angle on the scale for the other side. This value represents the angle regardless of side length. Angle measurement classification is typically based on side width. This process demonstrates a principle; angle size is independent of side length a concept with significant implications, in geometry studies and applications.
Examples of acute, obtuse, right and planar angles
Acute angles
Those angles, with a measurement, under 90 degrees or one quarter of a rotation fall into this category. This grouping includes an array of angles that play roles in different fields of math and physics. Equilateral triangles, which feature three sides of length always consist of three 60 degree angles. All angles, showcasing geometric harmony and equilibrium perfectly.




Obtuse angles
Angles, with a measurement than 90 degrees but than 180 degrees are commonly known as obtuse angles. When one of the two lines extends past the vertex it creates an angle that combined forms an angle measuring 180 degrees. If both half lines extend beyond the vertex two pairs of angles, opposite each other will total 360 degrees forming an angle referred to as a perigon or complete rotation.






Right Angles
Angles that are 90 degrees are known as angles. They are often represented by a square, at the vertex, than a curved arc distinguishing them from other types of angles. Every square and rectangle contains four angles emphasizing their geometric nature totaling 360 degrees for a complete rotation around a point.



Flat angles
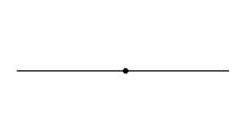
Angles that measure 180° represent half a turn showing a division, between two directions. Essentially these angles create the impression of a line extending infinitely emphasizing the idea of uninterrupted linear progression. An easy to visualize instance of an angle is the position of clock hands at 6;00 highlighting how straight angles are ingrained in our experiences and fundamental, to timekeeping.


FAQs
What is an acute angle?
An acute angle is an angle that measures less than 90 degrees.
Can you provide an example of an acute angle?
An example of an acute angle is 45 degrees.
What is an obtuse angle?
An obtuse angle is an angle that measures more than 90 degrees but less than 180 degrees.
Give an example of an obtuse angle
An example of an obtuse angle is 120 degrees.
What is a right angle?
A right angle is an angle that measures exactly 90 degrees.
Can you give an example of a right angle?
A classic example of a right angle is the corner of a square.
What is a flat angle?
A flat angle, also known as a straight angle, measures exactly 180 degrees.
Can you provide an example of a flat angle?
You can observe an angle when two lines form a line with the angle, between them being 180 degrees.
How can you identify an acute angle?
An acute angle is identified by its measurement being less than 90 degrees.
What is the sum of an acute angle and an obtuse angle?
The sum of an acute angle and an obtuse angle is always less than 180 degrees.
Can an angle be both acute and obtuse?
No, an angle cannot be both acute and obtuse at the same time.
How can you differentiate between a right angle and an obtuse angle?
A right angle measures exactly 90 degrees, while an obtuse angle measures more than 90 degrees.
What shapes often have right angles?
Shapes like squares, rectangles, and right-angled triangles have right angles.
Can a flat angle be found in geometric shapes?
Yes, a flat angle can be found in shapes like a straight line or in polygons with straight sides.
How are acute, obtuse, right, and flat angles used in real-life applications?
Angles like these are commonly applied in architecture, engineering and design to craft buildings and objects, with angles and measurements.